Odds
En algunos contextos, las probabilidades se presentan en forma de odds. La traducción más común en castellano es momios, pero se usan otras: posibilidades, oportunidades, ocasiones… Aquí usaremos odds.
Las odds de un suceso \(A\) son \[
\text{Odds}(A)=\frac{P(A)}{P(A^c)}=\frac{P(A)}{1-P(A)}
\] y por lo tanto nos dicen cuántas veces es más probable \(A\) que “no \(A\)”.
Si \(\text{Odds}(A)=q\), significa que por cada vez que ocurre “no \(A\)”, ocurre \(q\) veces \(A\). Por ejemplo, si las odds de suspender una asignatura son 2/3, significa que:
Por cada estudiante que aprueba, hay 2/3 de estudiante que suspenden.
Por cada 3 estudiantes que aprueban, hay 2 que suspenden.
De cada 5 estudiantes, 3 aprueban y 2 suspenden.
2 de cada 5 estudiantes suspenden.
La probabilidad de suspender es de un 40%.
A veces, que unas odds valgan \(a/b\) se expresa diciendo que son \(a\!:\!b\), y se lee “\(a\) a \(b\)”. Por ejemplo, las odds de suspender anteriores son 2:3, es decir, 2 a 3.
Ejemplo:
Algunos ejemplos de odds a partir de probabilidades:
- Si \(P(A)=0.2\), \(\text{Odds}(A)=0.2/0.8=0.25\).
- Si \(P(A)=0\), \(\text{Odds}(A)=0\).
- Si \(P(A)=0.5\), \(\text{Odds}(A)=1\).
- Si \(P(A)=1\), \(\text{Odds}(A)=\infty\).
Como son un cociente de dos probabilidades, las odds de un suceso son siempre mayores o iguales que 0 y pueden tomar cualquier valor entre 0 e \(\infty\), ambos incluidos.
Ejercicio Si lanzamos un dado equilibrado de 10 caras numeradas del 0 al 9:
¿Qué valen las odds de sacar un 3?
¿Qué valen las odds de sacar un múltiplo de 3?
Si sabemos las odds de \(A\), podemos calcular la probabilidad \(P(A)\): \[
\begin{array}{rl}
\text{Odds}(A)=\dfrac{P(A)}{1-P(A)}\!\!\!\! & \Longrightarrow \text{Odds}(A)-\text{Odds}(A)P(A)=P(A)\\
& \Longrightarrow P(A)=\dfrac{\text{Odds}(A)}{1+\text{Odds}(A)}
\end{array}
\]
Por lo tanto, dos sucesos tienen la misma probabilidad si, y solo si, tienen las mismas odds.
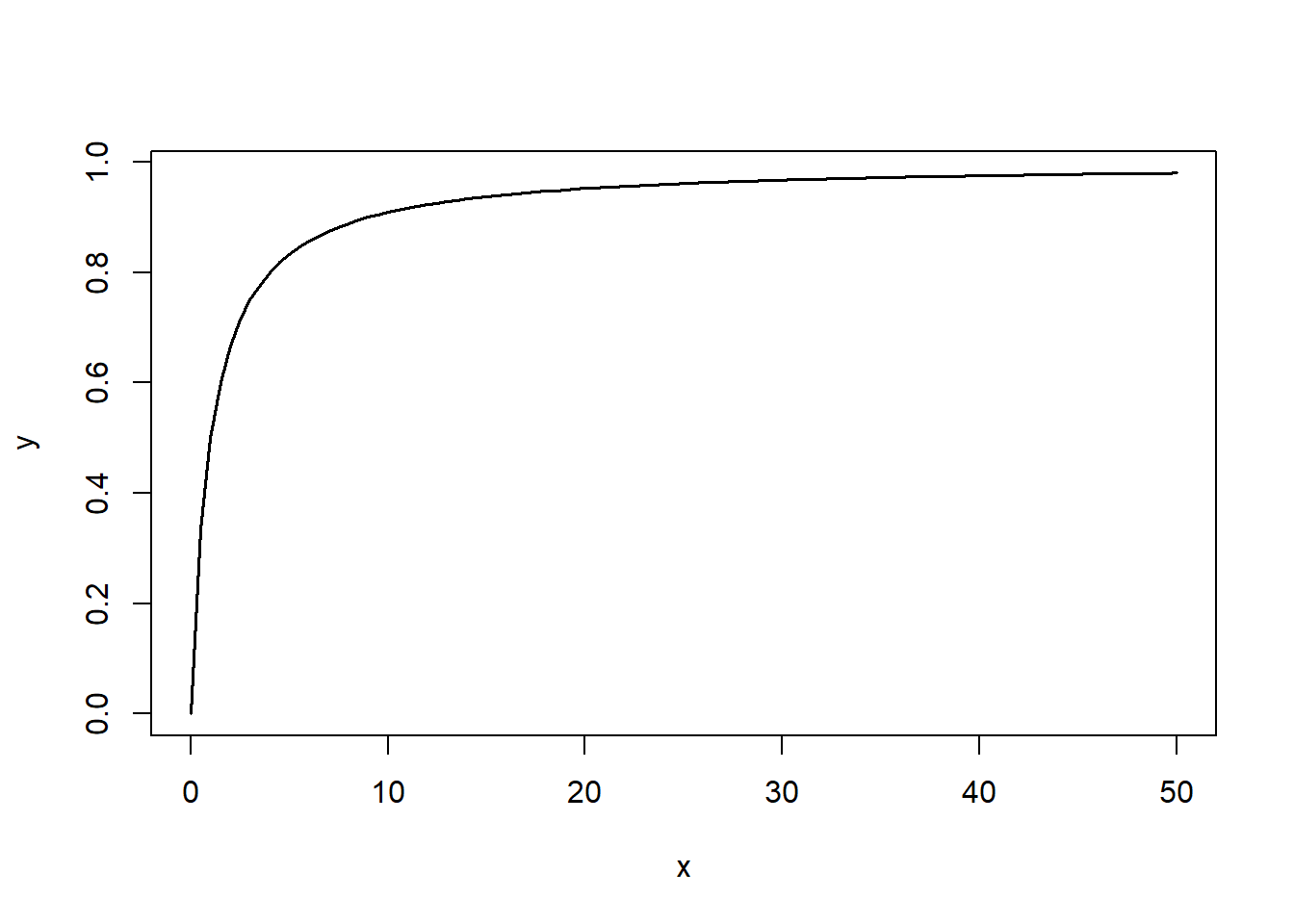
Observad que la función \[
x\mapsto\frac{x}{1+x}
\] es creciente en \(x\):
Como esta es la función que transforma \(\text{Odds}(A)\) en \(P(A)\), deducimos que \[
\text{Odds}(A)>\text{Odds}(B)\Longleftrightarrow P(A)>P(B)
\]
\(A\) es más probable que \(B\) si, y solo si, las odds de \(A\) son mayores que las de \(B\).
Como veremos, la manera correcta de presentar los resultados en los estudios de casos y controles es en forma de odds ratios. La odds ratio (razón de momios, de oportunidades…) de dos sucesos \(A\) y \(B\) es el cociente de sus odds: \[
\text{OR}(A,B)=\frac{\text{Odds}(A)}{\text{Odds}(B)}
\] Es decir, \(\text{OR}(A,B)\) nos dice cuántas veces son mayores (o menores) las odds de \(A\) que las de \(B\). Su valor es difícil de interpretar en términos de probabilidades excepto por lo que refiere a su relación con 1:
\(\text{OR}(A,B)=1\Longleftrightarrow \text{Odds}(A)=\text{Odds}(B) \Longleftrightarrow P(A)=P(B)\)
\(\text{OR}(A,B)>1\Longleftrightarrow \text{Odds}(A)>\text{Odds}(B) \Longleftrightarrow P(A)>P(B)\)
\(\text{OR}(A,B)<1\Longleftrightarrow \text{Odds}(A)<\text{Odds}(B) \Longleftrightarrow P(A)<P(B)\)
Pero, por ejemplo \[
\text{OR}(A,B)=2 \Longleftrightarrow \text{Odds}(A)= 2\cdot \text{Odds}(B) \hspace{1.2ex}
\not\hspace{-1.2ex}\Longleftrightarrow P(A)=
2\cdot P(B)
\]
Ejemplo:
En un estudio de casos y controles (Y. Nobel et al, Gastroenterology 159 (2020), pp. 373-375) se afirma que
“la presencia de síntomas gastrointestinales se asoció a un incremento del 70% en el riesgo de dar positivo [en el test de COVID-19]: odds ratio, 1.7.”
¿Qué significa esto? Que la odds ratio valga 1.7 significa que las odds de dar positivo en COVID-19 si se tienen síntomas gastrointestinales son 1.7 veces las de dar positivo si no se tienen síntomas gastrointestinales, es decir un 70% mayores. Pero fijaos que estamos hablando de las odds, no del riesgo entendido en el sentido de probabilidad. No tiene por qué ser cierto que la probabilidad de dar positivo en COVID-19 si se tienen síntomas gastrointestinales sea un 70% mayor que si no se tienen síntomas gastrointestinales.
De hecho, en este estudio concreto se obtuvo la tabla de frecuencias siguiente (SG abrevia “síntomas gastrointestinales”) \[
\begin{array}{r|c|c|c}
& \text{COVID-19 } + & \text{COVID-19 } - & \text{Total}\\ \hline
\text{SG Sí} & 97& 63 & 160\\\hline
\text{SG No} & 181 & 175 & 356\\\hline
\text{Total} & 278 & 238 & 316
\end{array}
\]
Por lo tanto, la proporción de COVID-19 positivos entre los que tuvieron síntomas gastrointestinales fue 97/160=0.606 y la proporción de COVID-19 positivos entre los que no tuvieron síntomas gastrointestinales fue 181/356=0.508. Como 0.606/0.508=1.19, la primera es un 19% mayor que la segunda, no un 70% mayor.
Veamos las odds. Las de ser COVID-19 positivo entre los que tuvieron síntomas gastrointestinales son \[
\frac{97/160}{63/160}=1.54
\] Las de ser COVID-19 positivo entre los que no tuvieron síntomas gastrointestinales son \[
\frac{181/356}{175/356}=1.03
\] La odds ratio es, entonces 1.54/1.03=1.495.
¿Pero no habíamos dicho que la odds ratio les había salido 1.7?
Bueno, sí, lo que les da 1.7 es la odds ratio ajustada, ORa, una odds ratio que se obtiene al descontar la influencia de confundidores en el desenlace.
Probabilidad condicionada
Dados dos sucesos \(A\) y \(B\), con \(P(A)>0\), la probabilidad de \(B\) condicionada a \(A\) es \[
P(B|A)=\frac{P(A\cap B)}{P(A)}
\]
Este valor representa la fracción de los sujetos de \(A\) que pertenecen a \(B\); es decir, es la probabilidad de que si ocurre \(A\), entonces también ocurra \(B\).
Ejemplo:
Supongamos que en una clase de 20 hombres y 30 mujeres, 15 hombres y 18 mujeres llevan gafas. La tabla de frecuencias correspondiente es
\[
\begin{array}{r|c|c|c}
& \text{Gafas} & \text{No gafas} & \text{Total}\\ \hline
\text{Mujeres} & 18 &12 & 30\\ \hline
\text{Hombres} & 15 & 5 & 20 \\ \hline
\text{Total} & 33 & 17 & 50 \\
\end{array}
\]
- ¿Cuál es la probabilidad de que un estudiante sea mujer?
Como hay 30 mujeres de un total de 50 estudiantes, esta probabilidad es 30/50=0.6
- ¿Cuál es la probabilidad de que un estudiante lleve gafas?
Como hay 33 estudiantes con gafas de un total de 50 estudiantes, esta probabilidad es 33/50=0.66
- ¿Cuál es la probabilidad de que un estudiante sea mujer y lleve gafas?
Como la probabilidad de ser mujer es 0.6 y la probabilidad de llevar gafas es 0.66, la probabilidad de ser mujer y llevar gafas es el producto: 0.6·0.66=0.396.
¡No! En general, la probabilidad de la intersección NO es el producto de las probabilidades.
Calculémosla bien. Como hay 18 mujeres que llevan gafas de un total de 50 estudiantes, esta probabilidad es 18/50=0.36
- ¿Cuál es la probabilidad de que una mujer lleve gafas?
Como hay 18 mujeres que llevan gafas de un total de 30 mujeres, esta probabilidad es 18/30=0.6. Fijaos que este valor es igual a \[
P(\text{gafas}|\text{mujer})=\frac{P(\text{mujer y gafas})}{P(\text{mujer})}=\frac{18/50}{30/50}=\frac{18}{30}
\]
- Escogemos un estudiante al azar. ¿Cuál es la probabilidad de que si es mujer, entonces lleve gafas?
Es la misma pregunta que la anterior, por lo que la respuesta es la misma: 18/30=0.6.
- ¿Cuál es la probabilidad de que un estudiante que lleve gafas sea mujer?
Como hay 18 mujeres que llevan gafas de un total de 33 estudiantes que lleven gafas, esta probabilidad es 18/33=0.545. Fijaos, de nuevo, que este valor es igual a \[
P(\text{mujer}|\text{gafas})=\frac{P(\text{mujer y gafas})}{P(\text{gafas})}=\frac{18/50}{33/50}=\frac{18}{33}
\]
No confundáis:
\(P(B)\): La probabilidad de que un individuo de la población global \(\Omega\) pertenezca a \(B\).
Por ejemplo, si \(B\) es “llevar gafas”, \(P(B)\) es la probabilidad de que una persona lleve gafas. La población en la que calculamos probabilidades es la de todas las personas.
\(P(B|A)\): Probabilidad de que un individuo de \(A\) pertenezca a \(B\).
Por ejemplo, si además \(A\) es “ser mujer”, \(P(B|A)\) es la probabilidad de que una mujer lleve gafas. La población en la que calculamos probabilidades es la de las mujeres.
\(P(A|B)\): Probabilidad de que un individuo de \(B\) pertenezca a \(A\).
Por ejemplo, con las notaciones anteriores, \(P(A|B)\) es la probabilidad de que una persona que lleva gafas sea mujer. La población en la que calculamos probabilidades es la de las personas que llevan gafas.
\(P(B\cap A)\): Probabilidad de que un individuo de la población global pertenezca simultáneamente a \(A\) y a \(B\).
Por ejemplo, con las notaciones anteriores, \(P(A\cap B)\) es la probabilidad de que una persona sea mujer y lleve gafas. La población en la que calculamos probabilidades vuelve a ser todas las personas.
Ejercicio:
En una universidad, los alumnos se distribuyen de la manera siguiente por tipos de estudios y sexos: \[
\begin{array}{r|c|c|c|c|c}
\text{Estudio} & \text{Ciencias} & \text{Derecho} & \text{Educación} & \text{Otros} & \text{Total}\\ \hline
\text{Hombres} & 1200 & 1300 & 300 & 2000 & 4800\\ \hline
\text{Mujeres} & 1400 & 600 & 1600 & 1600 & 5200\\ \hline
\text{Total} & 2600 &1900 & 1900 & 3600 & 10000\\
\end{array}
\]
Si escojo un estudiante al azar, ¿cuál es la probabilidad de que:
- Sea hombre o mujer?
- Sea mujer?
- Estudie Ciencias?
- No estudie Ciencias?
- Sea mujer o estudie Derecho?
- Sea mujer y estudie Derecho?
- Sea mujer pero no estudie Derecho?
- Si estudia Educación, sea mujer?
- Si es mujer, estudie Educación?
- Si es mujer, no estudie Educación?
- Si no es mujer, estudie Educación?
La probabilidad condicionada a \(A\), \(P(\ldots|A)\), es una probabilidad “de verdad”, simplemente hemos cambiado la población de \(\Omega\) a \(A\). Es decir, en vez de trabajar con proporciones de la población total \(\Omega\), trabajamos con proporciones de la subpoblación definida por los sujetos de \(A\). Por lo tanto, \(P(\ldots |A)\) satisface todas las propiedades de las probabilidades. Por ejemplo, se cumple que:
- \(P(B^c|A)=1-P(B|A)\)
- \(P(C-B|A)=P(C|A)-P(B\cap C|A)\)
- \(P(B\cup C|A)=P(B|A)+P(C|A)-P(B\cap C|A)\)
Ejemplo:
Supongamos que un 15% de los adultos son hipertensos, un 25% de los adultos creen que son hipertensos, y un 9% de los adultos son hipertensos y creen que lo son.
Si un adulto cree que es hipertenso, ¿cuál es la probabilidad de que lo sea?
Si un adulto es hipertenso, ¿cuál es la probabilidad de que crea que lo es?
Si un adulto no cree que sea hipertenso, ¿cuál es la probabilidad de que sí lo sea?
Pongamos nombres a los sucesos involucrados en estas preguntas:
\(A\): Ser hipertenso; \(P(A)=0.15\)
\(B\): Creer ser hipertenso; \(P(B)=0.25\)
\(A\cap B\): Ser hipertenso y creerlo; \(P(A \cap B)=0.09\)
En la primera pregunta nos piden la probabilidad de \(A\) condicionada a \(B\): \[
P(A|B)=\frac{P(A\cap B)}{P(B)}=\dfrac{0.09}{0.25}=0.36
\] Si un adulto cree ser hipertenso, tiene una probabilidad del 36% de serlo.
En la segunda pregunta nos piden la probabilidad de \(B\) condicionada a \(A\): \[
P(B|A) =\frac{P(A\cap B)}{P(A)}=\frac{0.09}{0.15}=0.6
\] Si un adulto es hipertenso, tiene una probabilidad del 60% de creer que lo es.
Y en la tercera pregunta nos piden la probabilidad de \(A\) condicionada a \(B^c\): \[
P(A|B^c) =\frac{P(A\cap B^c)}{P(B^c)}=\frac{P(A)-P(A\cap B)}{1-P(B)}=\frac{0.06}{0.75}=0.08
\] Si un adulto no cree ser hipertenso, tiene una probabilidad del 8% de ser hipertenso.
Ejemplo:
Un test para el VIH da positivo en un 99% de los casos en los que el virus está presente. En una población con el 0.5% de infectados por VIH:
¿Cuál es la probabilidad de que si hacemos el test a un infectado, dé positivo?
¿Cuál es la probabilidad de que hagamos el test a un infectado y dé positivo?
La respuesta a la primera pregunta nos la dan en el enunciado: “el test da positivo en un 99% de los casos en los que el virus está presente”, por lo que “la probabilidad de que si hacemos el test a un infectado, dé positivo” es 0.99.
Pero la segunda pregunta no pide lo mismo que la primera, sino la probabilidad de que pasen dos cosas: que hagamos el test a un infectado Y que dé positivo. Es la probabilidad de una intersección.
Pongamos nombres:
\(A\): Estar infectado; \(P(A)=0.005\)
\(B\): Dar positivo. De este suceso, sabemos solo la probabilidad condicionada \(P(B|A)=0.99\)
\(A\cap B\): Estar infectado y dar positivo. Es el suceso del que nos piden la probabilidad. \[
P(B|A)=\frac{P(A \cap B)}{P(A)}\Longrightarrow P(A \cap B)=P(B|A)\cdot P(A)=0.99\cdot 0.005=0.00495
\]
La probabilidad de que, al hacer el test a un individuo al azar, dé positivo y esté infectado es del 0.495%.
Ejemplo:
Un amigo cardiólogo nos contó una vez que la mitad de los enfermos que acudían a su consulta por supuestos problemas de corazón tenían en realidad estrés, y dos tercios, depresión. Nosotros vamos a suponer además que sólo un 15% de estos enfermos no sufrían ninguna de estas dos condiciones.
- ¿Cuál es la probabilidad de que un enfermo de estos tenga estrés si tiene depresión?
- ¿Cuál es la probabilidad de que un enfermo de estos no tenga estrés si no tiene depresión?
Esta vez vamos a usar primero el método de frecuencias naturales. Vamos a suponer que tenemos una población de referencia de 300 personas que acuden al cardiólogo.
La mitad, 150, tienen estrés y las otras 150 no.
Dos tercios, 200, tienen depresión y 100 no.
Hay un 15% de la población, es decir, 45 sujetos que no tienen ninguna de las dos condiciones.
En resumen, por ahora tenemos que \[
\begin{array}{r|c|c|c}
& \text{Depresión} & \text{No depresión} & \text{Total}\\ \hline
\text{Estrés} & & & 150 \\ \hline
\text{No estrés} & & 45 & 150 \\ \hline
\text{Total} & 200 & 100 & 300\\
\end{array}
\]
Ahora:
- De los 150 que no tienen estrés, como 45 tampoco tienen depresión, hay 105 que sí que tienen depresión.
- De los 100 que no tienen depresión, como 45 tampoco tienen estrés, hay 55 que sí que tienen estrés.
- De los 150 que tienen estrés, como 55 no tienen depresión, hay 95 que sí tienen estrés.
Ya tenemos la tabla de frecuencias completa: \[
\begin{array}{r|c|c|c}
& \text{Depresión} & \text{No depresión} & \text{Total}\\ \hline
\text{Estrés} & 95 & 55 & 150 \\ \hline
\text{No estrés} & 105 & 45 & 150 \\ \hline
\text{Total} & 200 & 100 & 300\\
\end{array}
\] Y ahora:
Como hay 200 pacientes con depresión, de los cuales 95 tienen también estrés, la proporción de pacientes con depresión que tienen estrés es 95/200=0.475. Un 47.5% de los pacientes que tienen depresión, también tienen estrés.
Como hay 100 pacientes sin depresión, de los cuales 45 no tienen estrés, la proporción de pacientes sin depresión que tampoco tienen estrés es 45/100=0.45. Un 45% de los pacientes que no tienen depresión, tampoco tienen estrés
¿Cómo lo hubiéramos resuelto usando las propiedades de probabilidades? Pongamos nombres:
\(E\): Tener estrés; \(P(E)=0.5\)
\(D\): Tener depresión; \(P(D)=2/3\)
\(E^c \cap D^c\): No tener ni estrés ni depresión; \(P(E^c\cap D^c)=0.15\)
Con estas notaciones, en la primera pregunta nos piden \[
P(E|D)=\dfrac{P(E\cap D)}{P(D)}
\] Para calcularla, necesitamos saber \(P(E\cap D)\), que vale: \[
P(E\cap D)=P(E)P(D)=0.5\cdot \frac{2}{3}=0.3333
\]
¡Que no! ¡Que la probabilidad de la intersección NO es en general igual al producto de las probabilidades!
Habrá que currárselo algo más:
\(P((E\cup D)^c)=P(E^c\cap D^c)=0.15\), por lo tanto \(P(E\cup D)=1-P((E\cup D)^c)=0.85\)
\(P(E\cap D)=P(E)+P(D)-P(E\cup D)=0.5+2/3-0.85=0.31667\)
Ahora sí, finalmente, \(P(E|D)=P(E\cap D)/P(D)=0.31667/0.66667=0.475\)
En la segunda pregunta nos piden \[
P(E^c|D^c)=\dfrac{P(E^c\cap D^c)}{P(D^c)}
\] y esta probabilidad ya la podemos calcular, porque sabemos que \(P(E^c\cap D^c)=0.15\) y \(P(D^c)=1-P(D)=1-2/3=1/3\), por lo que \(P(E^c|D^c)=P(E^c\cap D^c)/P(D^c)=0.15/(1/3)=0.45\).
Sucesos independientes
Dos sucesos \(A\) y \(B\) (ambos de probabilidad no 0) son independientes cuando \(P(B|A)=P(B)\). Es decir:
- Cuando pertenecer a \(A\) no modifica la probabilidad de pertenecer a \(B\).
- Cuando que ocurra \(A\) no modifica la probabilidad de que ocurra \(B\).
- Cuando la proporción de sujetos de \(B\) dentro de \(A\) es la misma que dentro del total de la población.
En esta definición los papeles de \(A\) y \(B\) son intercambiables, como muestra el resultado siguiente que, además, da una caracterización alternativa muy importante.
Dados dos sucesos \(A,B\), ambos de probabilidad ni 0 ni 1, las cinco condiciones siguientes son equivalentes:
- \(P(A \cap B)=P(A)\cdot P(B)\)
- \(P(B|A)=P(B)\)
- \(P(A|B)=P(A)\)
- \(P(B|A)=P(B|A^c)\)
- \(P(A|B)=P(A|B^c)\)
En efecto, fijaos en que, por la definición de probabilidad condicionada, \[
\begin{array}{l}
\mathbf{P(B|A)=P(B)} \Longleftrightarrow \dfrac{P(A\cap B)}{P(A)}=P(B)\\ \qquad \Longleftrightarrow
\mathbf{P(A\cap B)=P(A)\cdot P(B)}
\\ \qquad \Longleftrightarrow \dfrac{P(A\cap B)}{P(B)}=P(A)\\ \qquad \Longleftrightarrow
\mathbf{P(A|B)=P(A)}
\end{array}
\] Esto demuestra (a) \(\Leftrightarrow\) (b) \(\Leftrightarrow\) (c). Por otro lado \[
\begin{array}{l}
\mathbf{P(B|A)=P(B|A^c)}\Longleftrightarrow \dfrac{P(A\cap B)}{P(A)}=\dfrac{P(A^c\cap B)}{P(A^c)}\\ \qquad \Longleftrightarrow
P(A\cap B)P(A^c)=P(A^c\cap B)P(A)=P(B-A)P(A)\\ \qquad \Longleftrightarrow
P(A\cap B)(1-P(A))=(P(B)-P(A\cap B))P(A)\\ \qquad \Longleftrightarrow
P(A\cap B)-P(A\cap B)P(A)=P(B)P(A)-P(A\cap B)P(A)\\ \qquad \Longleftrightarrow
\mathbf{P(A\cap B)=P(B)P(A)}
\end{array}
\] lo que demuestra (a) \(\Leftrightarrow\) (d). La equivalencia (a) \(\Leftrightarrow\) (e) se demuestra intercambiando los papeles de \(A\) y \(B\) en la equivalencia (a) \(\Leftrightarrow\) (d).
Es decir, las afirmaciones siguientes son equivalentes entre si, y definen la independencia de \(A\) y \(B\):
La proporción de sujetos de \(B\) dentro de \(A\) es la misma que dentro del total de la población.
La proporción de sujetos de \(B\) dentro de \(A\) es la misma que dentro del complementario de \(A\)
La proporción de sujetos de \(A\) dentro de \(B\) es la misma que dentro del total de la población.
La proporción de sujetos de \(A\) dentro de \(B\) es la misma que dentro del complementario de \(B\).
La proporción de sujetos que son simultáneamente de \(A\) y de \(B\) es el producto de la proporción de sujetos de \(A\) por la proporción de sujetos de \(B\).
A partir del resultado anterior, se deduce fácilmente que las condiciones siguientes son equivalentes:
- \(A\) y \(B\) son independientes.
- \(A^c\) y \(B\) son independientes.
- \(A\) y \(B^c\) son independientes.
- \(A^c\) y \(B^c\) son independientes.
Es razonable. Decir que la probabilidad de que pase \(A\) no depende de si pasa \(B\) o no (\(A\) y \(B\) independientes), es lo mismo que decir que la probabilidad de que pase \(A\) no depende de que no pase \(B\) o sí pase (\(A\) y \(B^c\) independientes). Y si la probabilidad de que pase \(A\) no depende de que pase \(B\) o no, la probabilidad de que no pase \(A\) tampoco depende de que pase \(B\) o no.
Hemos dado la definición de independencia para sucesos de probabilidad no nula. Para cubrir todos los casos, un suceso de probabilidad 0 se considera siempre independiente de cualquier otro. Es razonable, porque si \(P(A)=0\), entonces, como \(A\cap B\subseteq A\), también \(P(A\cap B)=0\) para cualquier suceso \(B\), y se cumple entonces que \(P(A\cap B)=P(A)P(B)\).
La fórmula \(P(A\cap B)=P(A)P(B)\) es válida cuando \(A\) y \(B\) son independientes.
Más en general, dada una familia de sucesos \(A_1,\ldots,A_n\), diremos que son independientes cuando, para todo subconjunto de índices \(\{i_1,\ldots,i_k\}\subseteq \{1,2,\ldots,n\}\) se tiene que \[
P(A_{i_1}\cap\cdots \cap A_{i_k})=P(A_{i_1})\cdots P(A_{i_k})
\]
Ejemplo:
En los EEUU, un 33% de la población es hipertensa. Supongamos que escogemos al azar un estadounidense y le hacemos lanzar una moneda equilibrada. ¿Cuál es la probabilidad de que sea hipertenso y saque cara?
Consideremos los sucesos:
La probabilidad que queremos calcular es \(P(A\cap B)\): la probabilidad de que el sujeto sea hipertenso y saque cara.
Naturalmente, ser hipertenso y sacar cara son sucesos independientes: la probabilidad de que salga cara no tiene nada que ver con la tensión arterial de quien la lanza. Por lo tanto \[
P(A\cap B)=P(A)\cdot P(B)=0.33\cdot 0.5=0.165
\] La probabilidad de que el estadounidense escogido al azar sea hipertenso y saque cara es del 16.5%.
Ejemplo:
En los EEUU, el 36.5% de la población adulta es obesa, el 33% es hipertensa, y el 49.5% es obesa o hipertensa (datos del Centro de Control de Enfermedades, CDC, 2014). ¿Son la obesidad y la hipertensión sucesos independientes?
Consideremos los sucesos:
Queremos saber si es verdad que \(P(A\cap B)=P(A)P(B)\). Para ello tenemos que calcular \(P(A\cap B)\) a partir de los datos que tenemos: \[
P(A \cap B) =P(A)+P(B)-P(A\cup B)=0.365+0.33-0.495=0.2
\]
Por otro lado, \(P(A)\cdot P(B)= 0.365\cdot 0.33=0.12\)
Por lo tanto, son sucesos dependientes. De hecho, \(P(B|A)=0.2/0.365=0.55> 0.33=P(B)\): la probabilidad de ser hipertenso entre los obesos es mayor que en el global de la población estadounidense.
Ejemplo:
Un cierto test da positivo en un 10% de los individuos que no tienen una determinada enfermedad. Si a un individuo sano se le realizan dos tests independientes, ¿cuál es la probabilidad de que ambos den positivo? ¿Y la de que alguno dé positivo?
Consideremos los sucesos:
- \(A_1\): El primer test da positivo sobre un individuo sano
- \(A_2\): El segundo test da positivo sobre un individuo sano
Sabemos que \(P(A_1)=P(A_2)=0.1\) y que, como las dos repeticiones del test son independientes, los sucesos \(A_1\) y \(A_2\) son independientes. Entonces:
La probabilidad que los dos den positivo es \[
P(A_1\cap A_2) =P(A_1)\cdot P(A_2) =0.1\cdot 0.1=0.01
\]
La probabilidad que alguno dé positivo es \[
\begin{array}{rl}
P(A_1\cup A_2)\!\!\!\! & =P(A_1)+P(A_2)-P(A_1\cap A_2)\\
& = 0.1+0.1-0.01=0.19
\end{array}
\]
Ejercicio:
Tenemos dos tests, A y B, para una determinada enfermedad. Sobre los individuos que tienen dicha enfermedad, el test A da positivo en un 95% de las ocasiones y el test B da positivo en un 90% de las ocasiones. Si a un individuo enfermo se le realizan los dos tests de manera independiente, ¿cuál es la probabilidad de que alguno dé positivo?
El teorema de la probabilidad total
Ejemplo:
Tenemos una población clasificada en dos subpoblaciones, A y B; por ejemplo, expuestos y no expuestos a un factor de riesgo. La subpoblación A representa un 20% de la población y la B el 80% restante. Un 50% de la subpoblación A y un 5% de la subpoblación B presentan una cierta característica X; por ejemplo, desarrollan una enfermedad.
¿Qué proporción de la población presenta dicha característica X?
Esta pregunta la podemos resolver fácilmente mediante el método de frecuencias naturales. Supongamos que nuestra población de referencia es de 1000 individuos. Entonces:
200 serán de la subpoblación A, de los cuales la mitad, 100, tendrán la característica X y los otros 100 no.
800 serán de la subpoblación B, de los cuales el 5%, 40, tendrán la característica X y los otros 760 no.
Obtenemos la tabla de frecuencias siguiente: \[
\begin{array}{r|c|c|c}
& A & B & \text{Total}\\\hline
X &100 & 40 &140\\ \hline
\text{No }X &100 & 760 &860\\\hline
\text{Total} &200 & 800 & 1000
\end{array}
\] Entonces la fracción de los sujetos del total de la población con la característica X es 140/1000, un 14%.
¿Cómo podríamos usar las propiedades de las probabilidades para calcular este valor? Pues simplemente teniendo en cuenta que, como los sucesos \(A\) y \(B\), definidos por las correspondientes subpoblaciones, son disjuntos y recubren toda la población, tenemos que \[
X=(X\cap A)\cup (X\cap B),\quad (X\cap A)\cap (X\cap B)=\emptyset
\] y por lo tanto \[
P(X)=P(X\cap A)+P(X\cap B)=P(X|A)P(A)+P(X|B)P(B).
\]
Como \(P(A)=0.2\), \(P(B)=0.8\), \(P(X|A)=0.5\) y \(P(X|B)=0.05\)
\[
P(X)=0.5\cdot 0.2+0.05\cdot 0.8=0.14.
\]
El ejemplo anterior es una aplicación del Teorema de la probabilidad total siguiente:
Si \(A\) y \(X\) son dos sucesos y \(0<P(A)<1\), \[
P(X)= P(X\cap A) +P(X\cap A^c)=P(A)\cdot P(X|A)+ P(A^c)\cdot P(X|A^c)
\]
Algunos de vosotros habréis usado en Bachillerato un diagrama de árbol como el siguiente para representar este teorema:
Luego se calcula la probabilidad de cada “hoja” del árbol como el producto de las probabilidades del camino que llega a ella desde \(\Omega\) y se calcula como \(P(X)\) la suma de las probabilidades de las hojas cuyo suceso contiene “\(\cap X\)”.
En el ejemplo anterior, este diagrama es
Más en general, llamaremos una partición (o estratificación, clasificación) de una población \(\Omega\) a una familia (finita) de sucesos no vacíos \(A_1,\ldots,A_n\) tales que
- Recubren todo \(\Omega\): \(\Omega=A_1\cup\cdots\cup A_n\).
- Dos a dos son disjuntos: Para cada \(i,j\in\{1,\ldots,n\}\), si \(i\neq j\), se tiene que \(A_i\cap A_j=\emptyset\).
Teorema: Si \(A_1\), …, \(A_n\) es una partición de la población, entonces, para todo suceso \(X\), \[
\begin{array}{rl}
P(X)\!\!\!\! & = P(X\cap A_1) +\cdots+P(X\cap A_n)\\ & =P(A_1)\cdot P(X|A_1)+\cdots+ P(A_n)\cdot P(X|A_n)
\end{array}
\] En la suma de la derecha, si algún \(A_i\) tiene probabilidad \(P(A_i)=0\), hay que tomar \(P(A_i)P(X|A_i)=0\).
Ejemplo:
Un test para el VIH da positivo un 99% de los casos en los que el virus está presente y en un 5% de los casos en los que el virus no está presente. En una población con el 0.5% de infectados por VIH, ¿cuál es la probabilidad de que un individuo escogido al azar dé positivo?
En primer lugar vamos a usar el teorema de la probabilidad total para calcular esta probabilidad. Sean los sucesos:
Entonces \[
\begin{array}{rl}
P(X) \!\!\!\! & =P(A)\cdot P(X|A)+P(A^c)\cdot P(X|A^c) \\
&=0.005\cdot 0.99+0.995\cdot 0.05=0.0547
\end{array}
\]
Usemos ahora la técnica de frecuencias naturales. Tomemos una población de referencia de 100,000 individuos.
Un 0.05% están infectados: 500 infectados y 99500 no infectados.
En un 99% de los infectados el test da positivo, son 495. En los 5 restantes da negativo.
En un 5% de los no infectados da positivo, son 4975. En los 94525 restantes da negativo.
La tabla de frecuencias resultante es
\[
\begin{array}{l|c|c|c}
& \text{Test }+ & \text{Test }- & \text{Total}\\
\hline
\text{VIH} & 495 & 5 & 500\\ \hline
\text{No VIH} & 4975& 94525 & 99500\\\hline
\text{Total} &5470 & 94530& 100000
\end{array}
\]
La proporción de personas en las que el test da positivo es 5470/100000=0.0547.
Ejemplo:
Un test diseñado para diagnosticar una determinada enfermedad da positivo el 94% de las veces en las que existe la enfermedad, y un 4% de las veces en las que no existe la enfermedad. A partir de un estudio masivo se estima que un 15% de la población da positivo en el test. ¿Cuál sería la prevalencia de la enfermedad?
Fijaos en que si llamamos \(E\) al suceso “Tener la enfermedad” y \(+\) al suceso “Dar positivo en el test”, los datos que tenemos son \(P(+)\), \(P(+|E)\) y \(P(+|E^c)\), y queremos saber \(P(E)\). Esta cuestión se resuelve fácilmente con el Teorema de la Probabilidad Total usando \(P(E)\) como incógnita: \[
\begin{array}{l}
P(+)=P(+|E)P(E)+(P+|E^c)P(E^c) \\
\qquad\Longrightarrow
0.15 =0.94 P(E)+0.04(1-P(E))
\end{array}
\] de donde podemos despejar \(P(E)\): \[
0.11=0.9P(E)\Rightarrow P(E)=\frac{0.11}{0.9}=0.1222
\]
También podemos usar la técnica de frecuencias naturales. Tomamos una población de referencia de 100,000 individuos. De ellos, un 15%, 15,000, dan positivo en el test, y los 85,000 restantes, negativo.
Llamemos \(x\) al número de enfermos, de manera que \(100000-x\) es el número de sanos. Sabemos que un 94% de los enfermos y un 4% de los sanos dan positivo. Por lo tanto, el número de enfermos positivos será igual a \(0.94x\) y el número de sanos \(0.04(100000-x)\). Completando la tabla para que las sumas de las filas sean correctas, obtenemos:
\[
\begin{array}{l|c|c|c}
& \text{Test }+ & \text{Test }- & \text{Total}\\
\hline
\text{Enfermo} & 0.94x & 0.06x & x \\ \hline
\text{Sano} & 0.04(100000-x) & 0.96(100000-x) & 100000-x \\\hline
\text{Total} & 15000 & 85000 & 100000
\end{array}
\] Y ahora, por la primera columna, \[
\begin{array}{l}
15000=0.94x+0.04(100000-x)=0.9x+4000\\
\qquad\displaystyle \Longrightarrow x=\frac{11000}{0.9}=12222.22
\end{array}
\] Por lo tanto, la prevalencia de la enfermedad es 12222.22/100000=0.1222: un 12.22%.
Ejercicio:
En el estudio de Rotterdam, un 21.7% de la cohorte inicial eran fumadores, un 43% habían sido fumadores pero ya no lo eran, y un 35.3% nunca habían fumado. En el primer grupo, un 26% desarrolló EPOC durante el seguimiento; entre el segundo grupo, un 13.6%, y en el tercero, un 6.4%.
¿Qué porcentaje de la cohorte desarrolló EPOC durante el seguimiento?
Vamos a llamar “fumador” a un sujeto de la cohorte que o fumaba al principio del estudio, o había fumado anteriormente pero lo había dejado. ¿Qué porcentaje de estos fumadores desarrolló EPOC durante el seguimiento?
El teorema de la probabilidad total se usa de manera implícita en el cálculo de tasas ajustadas:
- Se divide una población en estratos (sexo, grupos étnicos, franjas de edad…).
- Se calcula la proporción de algo en cada estrato.
- Se deduce la proporción ajustada de ese algo en una población que tuviera una composición estándar de esos estratos.
Por ejemplo, para obtener la tasa de mortalidad de una enfermedad en España ajustada a la composición en franjas de edad de la Unión Europea:
Se obtiene la tasa de mortalidad de la enfermedad por franjas de edad en España.
Se toma como composición en franjas de edad la de la Unión Europea.
Se calcula la tasa de mortalidad de esa enfermedad en una población cuya composición en franjas de edad fuera la europea y en la que la tasa de mortalidad en cada franja de edad fuera la española.
Calculando estas tasas ajustadas para varios países de la UE, se pueden comparar sus tasas de mortalidad evitando el factor de confusión que podría representar la edad.
Ejemplo:
Una cierta enfermedad tiene en China una tasa de mortalidad del 0.1% entre los menores de 15 años, del 0.3% entre las personas de 15 a 64 años y de un 0.7% entre los mayores de 65 años. En la Unión Europea, un 15.5% de la población es menor de 15 años, un 65.4% tiene entre 15 y 64 años, y un 19.1% tiene 65 años o más. En China, estas proporciones son del 17.6%, 71.2% y 11.2%, respectivamente
¿Cuál es la tasa de mortalidad de esta enfermedad en China? ¿Cuál sería la tasa de mortalidad de esta enfermedad ajustada a la distribución de edades de la Unión Europea?
Pongamos nombres a los sucesos de interés:
\(M\): Morir de la enfermedad
\(C_1\): Tener menos de 15 años en China; \(P(C_1)=0.176\)
\(C_2\): Tener entre 15 y 64 años en China; \(P(C_2)=0.712\)
\(C_3\): Tener 65 años o más en China; \(P(C_3)=0.112\)
\(E_1\): Tener menos de 15 años en la UE; \(P(E_1)=0.115\)
\(E_2\): Tener entre 15 y 64 años en la UE; \(P(E_2)=0.654\)
\(E_3\): Tener 65 años o más en la UE; \(P(E_3)=0.191\)
Tenemos que \(P(M|C_1)=0.001\), \(P(M|C_2)=0.003\) y \(P(M|C_3)=0.007\).
Por el teorema de la probabilidad total, la tasa de mortalidad en China es \[
\begin{array}{rl}
P(M)\!\!\!\! &=P(M|C_1)\cdot P(C_1)+P(M|C_2)\cdot P(C_2)+P(M|C_3)\cdot P(C_3)\\
& =0.001\cdot 0.176+0.003\cdot 0.712+0.007\cdot 0.112=0.0031
\end{array}
\] O sea, del 0.31%.
La tasa de mortalidad de esta enfermedad ajustada a la distribución de edades de la UE, \(\mathit{TA}\), sería la probabilidad de \(M\) en una población en la que cada franja de edad tuviera probabilidad como en la UE, \(P(E_i)\), y la tasa de mortalidad en cada franja de edad fuera como la de China, \(P(M|C_i)\):
\[
\begin{array}{rl}
\mathit{TA}\!\!\!\! & =P(M|C_1)\cdot P(E_1)+P(M|C_2)\cdot P(E_2)+P(M|C_3)\cdot P(E_3)\\
& =0.001\cdot 0.115+0.003\cdot 0.654+0.007\cdot 0.191=0.0034
\end{array}
\] Es decir, esta tasa de mortalidad ajustada a la UE es del 0.34%. Es un poco mayor que la “real” en China. Es razonable: vemos que la tasa de mortalidad crece con la edad, y la UE tiene una menor proporción de niños y una mayor proporción de ancianos que China.
Ejercicio:
Supongamos que en los Emiratos Árabes, donde hay 256 hombres por cada 100 mujeres (en serio, datos del CIA Woldfact), un 1% de los hombres y un 2% de las mujeres sufren de una determinada enfermedad.
(b) ¿Cuál es la prevalencia de esta enfermedad en esta población?
(c) ¿Cuál es la prevalencia de esta enfermedad ajustada a una población con un 50% de cada sexo?
La regla de Bayes
A menudo conocemos las probabilidades condicionadas en una dirección pero las que nos interesa saber son precisamente las probabilidades condicionadas en la dirección opuesta. Por ejemplo:
En un estudio de casos y controles hemos estimado las probabilidades de que individuos sanos y enfermos hayan estado expuestos al factor de riesgo, pero lo que queremos saber son las probabilidades de que individuos expuestos y no expuestos enfermen.
Podemos conocer las proporciones de individuos sanos y enfermos que dan positivo en un test diagnóstico, pero lo interesante es la probabilidad de estar enfermo si das positivo en el test (o de estar sano si das negativo).
Ejemplo:
Una mujer de 45 años da positivo en una mamografía anual de cribado. Si una mujer tiene cáncer de mama, la probabilidad de dar positivo en dicha prueba es del 99%, y si no lo tiene, esta probabilidad es aún del 9%. Os pide cuáles son sus probabilidades de tener cáncer de mama. ¿Qué contestaríais?
Casi seguro, lo siento mucho.
Del orden de un 50%.
Del orden de un 10%.
Tranquila, del orden de un 1%.
Casi seguro de que no, del orden de un 0.1%.
¡Señora, yo estudié farmacia, no matemáticas!
Las preguntas de este tipo no pueden responderse sin alguna información extra. Por ejemplo, la probabilidad global de haber estado expuestos al riesgo o la prevalencia de la enfermedad en el ejemplo de los estudios de casos y controles, o la prevalencia de la enfermedad o la proporción global de positivos en el ejemplo del test diagnóstico.
Ejemplo:
Descartada la respuesta (f), buscáis por Internet y encontráis que, según el informe “Las cifras del cáncer en España 2020” de la Sociedad Española de Oncología Médica, la prevalencia del cáncer de mama en España en el período 2013-2018 fue de 130,000 casos de cáncer de mama entre los cerca de 24,000,000 de mujeres españolas. Eso os lleva a concluir que la prevalencia del cáncer de mama entre las mujeres españolas es de alrededor del 0.5%? ¿Qué responderíais a la pregunta de la mujer?
Este tipo de cuestiones se resuelve fácilmente por el método de frecuencias naturales.
Tomamos una población de referencia de 100,000 mujeres y calculamos la tabla de frecuencias en esta población correspondiente a la situación planteada.
Un 1% de la población tiene cáncer de mama: 1,000 mujeres. Las 99,000 restantes, no.
De las 1,000 mujeres con cáncer de mama, un 90% dan positivo en la mamografía: 900. Las 100 restantes, dan negativo
De las 99,000 mujeres sin cáncer de mama, un 10% dan positivo en la mamografía: 9,900. Las 89,100 restantes dan negativo.
La tabla de frecuencias resultante (donde “Test” indica la mamografía) es
\[
\begin{array}{l|c|c|c}
& \text{Test }+ & \text{Test }- & \text{Total}\\
\hline
\text{Cáncer Sí} & 900 & 100 & 1000\\ \hline
\text{Cáncer No} & 9900& 89100 & 99000\\\hline
\text{Total} &10800 & 89200& 100000
\end{array}
\]
Entonces, la proporción de mujeres con cáncer de mama entre las que dan positivo en la mamografía es de 900/10800= 0.0833: un 8.33%.
La fórmula de Bayes siguiente permite resolver este tipo de problemas sin tener que recurrir a las frecuencias naturales.
Teorema de Bayes: Sean \(A\) y \(B\) dos sucesos. Si \(P(A),P(B)>0\), entonces \[
P(A|B) =\dfrac{P(A)\cdot P(B|A)}{P(A)\cdot P(B|A)+P(A^c)\cdot P(B|A^c)}
\]
Esta fórmula se obtiene de \[
P(A|B) =\dfrac{P(A \cap B)}{P(B)}
\] donde \[
P(A \cap B)=P(A)\cdot P(B|A)
\] y, por el teorema de la probabilidad total, \[
P(B)=P(A)\cdot P(B|A)+P(A^c)\cdot P(B|A^c).
\]
Con los números del ejemplo, si llamamos \(C\) al suceso “Tener cáncer de mama” y \(M\) al suceso “Dar positivo en la mamografía”, tenemos que \(P(C)=0.01\), \(P(M|C)=0.9\) y \(P(M|C^c)=0.1\), y por lo tanto \[
\begin{array}{rl}
P(C|M)\!\!\!\! & =\dfrac{P(C)\cdot P(M|C)}{P(C)\cdot P(M|C)+P(C^c)\cdot P(M|C^c)}\\
& =\dfrac{0.01\cdot 0.9}{0.01\cdot 0.9+0.99\cdot 0.1}=0.0833
\end{array}
\]
Más en general, si \(A_1,A_2,\ldots,A_n\) es una partición de \(\Omega\) y \(X\) un suceso y todos estos sucesos tienen probabilidad no nula, entonces \[
P(A_i|X) =\dfrac{P(A_i)\cdot P(X|A_i)}{P(A_1)\cdot P(X|A_1)+\cdots+P(A_n)\cdot P(X|A_n)}
\]
Ejemplo:
Volvemos a la situación del ejemplo. Tenemos un test para el VIH que da positivo en un 99% de las personas en las que el virus está presente y en un 5% de las personas en las que el virus no está presente.
En una población con el 0.5% de infectados por VIH, ¿cuál es la probabilidad de que un individuo que haya dado positivo en el test esté infectado? ¿Y cuál es la probabilidad de que un individuo que haya dado negativo en el test no esté infectado?
Si llamamos \(A\) al suceso “Estar infectado por VIH” y \(B\) al suceso “Dar positivo en el test”, entonces:
- La probabilidad de que un individuo que dé positivo en el test esté infectado es \[
\begin{array}{rl}
P(A|B)\!\!\!\! & =\dfrac{P(B|A)\cdot P(A)}{P(B|A)\cdot P(A)+P(B|A^c)\cdot P(A^c)}\\
&=\dfrac{0.99\cdot 0.005}{0.99\cdot 0.005+0.05\cdot 0.995}=0.09
\end{array}
\]
Solo un 9% de los positivos están realmente infectados.
- La probabilidad de que un individuo que dé negativo en el test no esté infectado es \[
\begin{array}{rl}
P(A^c|B^c)\!\!\!\!& =\dfrac{P(B^c|A^c)\cdot P(A^c)}{P(B^c|A)\cdot P(A)+P(B^c|A^c)\cdot P(A^c)}\\
& =\dfrac{0.95\cdot 0.995}{0.01\cdot 0.005+0.95\cdot 0.995}=0.99995
\end{array}
\]
Un 99.995% de los negativos no están infectados.
Ejemplo:
Seguimos con el test para el VIH en una población con el 0.5% de infectados por VIH del ejemplo anterior. Supongamos ahora que a un individuo que da positivo le repetimos el test y vuelve a dar positivo. Si los resultados de las dos repeticiones del test son independientes ¿cuál es la probabilidad de que este individuo esté infectado?
Sea \(A\) al suceso “Estar infectado por VIH” y llamemos ahora \(B_2\) al suceso “Dar positivo en dos repeticiones independientes del test”. Si la probabilidad de que un infectado dé positivo en un test es 0.99, la probabilidad de que dé positivo en dos tests independientes será 0.99·0.99=0.9801 (el producto de la probabilidad de dar positivo en el primero por la probabilidad de dar positivo en el segundo). Y si la probabilidad de que un no infectado dé positivo en un test es 0.05, la probabilidad de que dé positivo en dos tests independientes será 0.05·0.05=0.0025.
Es decir, \(P(B_2|A)=0.9801\) y \(P(B_2|A^c)=0.0025\). Apliquemos de nuevo la fórmula de Bayes:
\[
\begin{array}{rl}
P(A|B_2)\!\!\!\! & =\dfrac{P(B_2|A)\cdot P(A)}{P(B_2|A)\cdot P(A)+P(B_2|A^c)\cdot P(A^c)}\\
&=\dfrac{0.9801\cdot 0.005}{0.9801\cdot 0.005+0.0025\cdot 0.995}=0.6633
\end{array}
\]
Con el segundo positivo, la probabilidad de infección ha subido del 9% al 66.33%.
En la vida real, esta segunda probabilidad seguramente sea menor, porque algunos pacientes libres de VIH tienen moléculas en la sangre similares a los anticuerpos del VIH que detecta el test y que dan lugar a falsos positivos; por ejemplo, personas con enfermedades autoinmunes como el lupus. En estos pacientes la repeticiones de los tests no se pueden considerar independientes.
Ejercicio: Un test de detección precoz de una enfermedad da positivo el 97.5% de las veces en que existe la enfermedad, y un 12% de las veces en que no existe la enfermedad. La probabilidad de que un individuo escogido al azar tenga esta enfermedad es de un 2%.
¿Cuál es la probabilidad de que un individuo escogido al azar dé positivo en el test?
¿Cuál es la probabilidad de que un individuo escogido al azar tenga la enfermedad y dé positivo en el test?
¿Cuál es la probabilidad de que un individuo que dé positivo en el test, tenga esta enfermedad?
El dar positivo en el test y el tener la enfermedad, ¿son sucesos independientes?